一、缘起

8月份的时候，现网使用的某应用使用的RSA算法进行加解密（管理端使用公钥加密，被管理端使用私钥解密），而后被我通过一些技术手段取得了公钥信息，进而写出了一个可以对接的crack小程序，在告诉相应的开发人员以后，其让为RSA是不可能被破解的，其实其忽略了RSA算法的基础。本篇就总结下我所了解的RSA加密。

二、RSA的历史

RSA-history
RSA-history

RSA的算法历史我将其分为三个块：

  • 理论基础块：最早源于1636年的费马小定理，几十年后的欧拉在验证费马小定理的基础上，提出了欧拉定理。而RSA算法就是在欧拉定理的基础上的应用。
  • 军用阶段：1973年英国的一位在英国政府通讯总部工作的数学家Clifford Cocks提出了一种类RSA的非对称加密数法，不过该算法直到1997年才公布；
  • 民用阶段：1976年美国的两位数学家提出了密钥交换算法，1977年三位在麻省理工学院工作的数学家一起研究出了RSA算法，而RSA的名称就是从三个人名字里各提了一个字母结合而成的。

殴拉定理如下：

1aφ(n)≡1(modn)

三、涉及的数学概念

1、涉及的数学名词

  • 公约数
  • 质数
  • 互质数
  • 欧拉定理

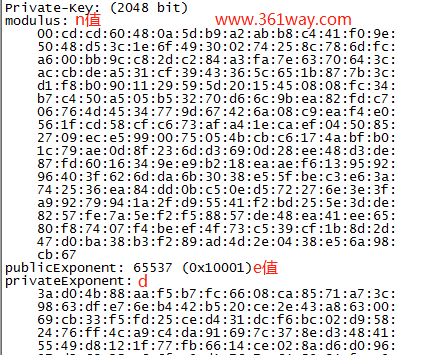
2、6个数值

在很多编程语言里用到的有三个值n、e、d ，ne的组合为rsa的公钥，nd为私钥。服务器将公钥发给客户端。在以后的加密解密中，公钥用于加密和签名验证，私钥用于解密与签名。加密数字K：计算C=(K^e)%n，C即为加密后的数据 解密C得到K：K=(C^d)%n ,签名采用相反的方式，即服务器用私钥加密，客户端用公钥解密，验证解密后的数据。

1　　p
2　　q
3　　n  modulus   模
4　　φ(n)
5　　e  exponents 指数
6　　d
7公钥 (n,e) 用于加密
8私钥 (n,d) 用于解密

相关计算公式如下：

3、相关理念

  1. 私钥可以推导出公钥
  2. RSA不是不可解的，只因取的整数比较大，进行因数分解比较难。

人类已经分解的最大整数（232个十进制位，768个二进制位），我们常用的1024和2048位都是指的二进制位。RSA相对还是安全的，768位的计算是在2010年左右公布的，是在上百台的计算机集群上运行了两年才解出的。RSA算法最大的杀手是量子计算，几百量子 的计算机，可以在数秒内解出1024位的因数分解。不过几百量子位算力的计算机能搞出来也不知道是什么时候的事了。

四、openssl rsa相关

1# 生成私钥
2openssl genrsa -out privatekey.txt 2048
3# 由私钥导出公钥
4openssl rsa -in privatekey.txt -pubout -out publickey.txt
5# 以n d e p q格式查看
6openssl pkey -in privatekey.txt -inform PEM -text

由于以n d e p q格式查看的输出转多，这里只输出部分。

inform.png
inform.png

利用该命令查看到私钥格式如下：

 1RSAPrivateKey ::= SEQUENCE {
 2  version           Version,
 3  modulus           INTEGER,  -- n
 4  publicExponent    INTEGER,  -- e
 5  privateExponent   INTEGER,  -- d
 6  prime1            INTEGER,  -- p
 7  prime2            INTEGER,  -- q
 8  exponent1         INTEGER,  -- d mod (p-1)
 9  exponent2         INTEGER,  -- d mod (q-1)
10  coefficient       INTEGER,  -- (inverse of q) mod p
11  otherPrimeInfos   OtherPrimeInfos OPTIONAL
12}

在文档 RFC3447 中定义了 RSA 密钥的语法结构，私钥的语法结构如上所示。 version 是 RSA 的版本号，本文中使用的密钥版本号是 0，如果密钥是使用多素数（多于 2 个素数）版本号则为 1。

1modulus 是 RSA 的合数模 n。
2publicExponent 是 RSA 的公开幂 e。
3privateExponent 是 RSA 的私有幂 d。
4prime1 是 n 的素数因子 p。
5prime2 i 是 n 的素数因子 q。
6exponent1 等于 d mod (p − 1)。
7exponent2 等于 d mod (q − 1)。
8coefficient 是 CRT 系数 q–1 mod p。
9otherPrimeInfos 按顺序包含了其它素数 r3，……，ru 的信息。如果 version 是 0 ，它应该被忽略；而如果 version 是 1，它应该至少包含 OtherPrimeInfo 的一个实例。

RSA 公钥的语法结构如下所示，可见公钥所需的因子信息都包含在私钥中：

1RSAPublicKey ::= SEQUENCE {
2 modulus INTEGER, -- n
3 publicExponent INTEGER -- e
4}

OpenSSH 的 RSA 密钥的文件体使用 DER 编码，JDK 提供了 DerInputStream 来解析 DER 编码的字符串。所以 OpenSSH 密钥的解析很简单，首先读取密钥，过滤掉开始和结束标志，文件头（如果是加密的密钥则需要根据文件头信息来确定解密方式，因本文使用未加密的密钥故去掉文件头），然后使用 DER inputstream 来解析密钥。

五、openssl与ssh-keygen

ssh-keygen就可以直接生成密钥认证对的，而openssl生成的密钥对能不能给ssh用呢？（因为大家都是走的RSA认证。）

答案是私钥可以直霎，公钥不可以直接用，通过转化可以用。因为openssl命令导出的公钥格式为PKCS8格式，而ssh key认证使用格式为RFC4716格式。

具体可以参看 https://tools.ietf.org/html/rfc4716

1ssh-keygen -f publickey.txt -e -m pkcs8 > key.pub
2From the ssh-keygen man page:
3-m key_format
4         Specify a key format for the -i (import) or -e (export) conversion
5         options.  The supported key formats are:
6         ``RFC4716'' (RFC 4716/SSH2 public or private key),
7         ``PKCS8'' (PEM PKCS8 public key) or
8         ``PEM'' (PEM public key).
9         The default conversion format is ``RFC4716''.

-m参数在RHLE7版本里有，在此之前的版本里没有该参数，即openssh-7.4版本里发现有。

上面在相关理念里有提到私钥可以推导出公钥，哪ssh生成的公钥如果丢了或者删除了，只有私钥能不能生成公钥呢？

这个是当然可以的，而且ssh-keygen命令已经帮我们实现了：

1# ssh-keygen -y -f mykey.pem > mykey.pub
2# ssh-keygen -y [-f input_keyfile]
3-y This option will read a private OpenSSH format file and print an OpenSSH public key to stdout.

use-rsa-private-key-to-generate-public-key

同时通过openssl 命令还可以直接查看模的值（输出太多了，这里也只是取了modules的一部分）：

1# openssl rsa  -modulus -in id_rsa
2Modulus=C6BC3A3968B61B1AB571783BDB325FE0430AD9EA3FFC10C03C6C4FAA64CDE6F10534F2B534C88C9689B2315BA6B88F33223FB4265B3F9C926F1F8E1

六、进制转换

在很多编程语言里，会发现，上面提到的n d e都是在代码里会以十进制形式存在，而上面的命令我们查看到的是十六进制，JAVA引用代码如下:

1PublicKey publicKey = Testclient.getPublicKey("98290099109057374932919249469161865256641935155149738301916331467469001708103109836087", "65537");
2encrypted = Testclient.encrypt(content, publicKey);

这个处理其实非常简单，将上面openssl 查看得到的值，通过十六进制和十进制之间的转换即可。

1>>> int('0x10001', 16)
265537
3>>> int('BEB90F8AF5D8A7C7DA8CA74AC43E1', 16)
461893117520429489358314352530965473L